Recent Notes
Pareto Frontier
Status: This was written in a hurry. I should find some way to label these with how much effort went into them / how much attention should be put on them…
The Pareto frontier can help you find a subset of your data points that are the ones that represent trade-offs between maximizing the various dimensions.
Imagine you’re looking at data about thousands of cars, and for each car you know its cost, mileage, and top speed. Maybe you’re trying to get a general sense of which cars perform the best, but this can be difficult when there are multiple attributes along which they can be compared.
All else being equal, though, you want a lower cost, higher mileage, and higher top speed, and it could be the case that some cars are strictly better than others on all three of these aspects. That set of those points is called the Pareto frontier.
The Pareto frontier will reveal the points that represent interesting trade-offs: no point on the frontier is strictly better than any other. Of course, there may be important real-world dimensions not captured in your data – perhaps you also care about the size of the car, for example – and in that case, looking at only the frontier of cost, mileage, and top speed can be a dangerous thing since it would cause you to ignore potentially relevant points along those other dimensions or skew your data (since size is correlated with all three dimensions). But if you can quantify these “hidden” aspects and add them to your data, the new higher-dimensional frontier might prove to be a source of insight.
Implementation
Here’s a simple JavaScript implementation of a Pareto frontier algorithm from the paper Fast Linear Expected-Time Algorithms for Computing Maxima and Convex Hulls., coauthored by Jon Bentley of Programming Pearls fame.
It takes an array of points, each represented by an array, and returns the indices of the points that are on the “max” Pareto frontier (intuitively, these points are generally “strictly larger” than the others when considering all dimensions).
// Return the indices of points on the max Pareto frontier (maxima of a point set) using algorithm
// M3 from "Fast Linear Expected-Time Algorithms for Computing Maxima and Convex Hulls".
// Note that if multiple equal points are potentially on the frontier, only one will be returned.
// p1 dominates p2 if it is greater than it in some components and equal
// in the remainder (incomparable in no components). Allows for dimensions
// s. t. neither p1 nor p2 is less than the other, eg. if the values
// are distinct Objects.
Cheerio for Web Scraping
A great JavaScript library has recently reached 1.0: Cheerio. It gives you a jQuery-like syntax for quickly parsing out content from an HTML string.
I recently used it to parse out some data from a structured list using a nice high-level DSL that’s used by Cheerio’s extract function.
;
// The page has many of these:
// <div class="ts-segment">
// <span class="ts-name">Jimmy Wales</span>
// <span class="ts-timestamp"><a href="https://youtube.com/watch?v=XXXX&t=5112">(01:23:45)</a> </span>
// <span class="ts-text">Hmm?</span>
// </div>
;
The input HTML content contains many snippets like the one in the comment above. One nice thing about Cheerio’s extract function is that if parts of a composite value are missing, then the entries in each segment will remain undefined while the existing values are extracted. For example, if the name is missing from a particular segment and its selector fails to match, then its timestamp, href, and text will still be extracted.
Running the extraction will return a JavaScript object with the key segments, whose value is an array of objects each with a name, timestamp, href, and text, mirroring the shape of the input.
One nice thing about this interface is its flexibility, which allows you to extract arbitrary properties at multiple levels of a nested tree-like query. The docs for the function aren’t very informative as to what can be extracted but this tutorial explains many of the possibilities, including using a function as the extractor.
Visualizing Sentences with Finite State Automata
The National Electronic Injury Surveillance System in the US collects data on product-related injuries. It has a dataset of emergency room visits, with granular information on over 8.5 million visits across 100 hospitals going back over 20 years.
An interesting feature of the data is that each ER visit comes with a narrative story. For example:
A 50YOF DROPPED A CRYSTAL BALL ON FOOT, SPRAINED FOOT
PATIENT ROLLED OFF BED, HIT EAR ON DRESSER OR ON WOODEN KNOB SHAPED LIKE AN ELEPHANT HEAD AT HOME; EAR LAC.
2 NIGHTS AGO A FRIEND MICROWAVED A MARSHMALLOW AND PUT IT ON PT’S NECKPT HAS BURN TO NECK WITH BLISTERING
One way to get a qualitative sense of what’s in this dataset is to do some thematic keyword searches. For example, for bicycles:
PT FELL OFF BICYCLE AND HIT HEAD
PT RIDING BICYCLE AND FELL AND LAC ARM
13YOBF FELL OFF BICYCLE;RADIAL HEAD FX
Avocados:
PT CUTTING AN AVOCADO AND LAC HAND ON KNIFE
LAC FINGER ON KNIFE CUTTING AVOCADO
CUT WITH KNIFE TO FINGER WHILE CUTTING AVOCADOSDX: LAC FINGER PT
Cowboy boots:
PT DANCING IN COWBOY BOOTS STRAINED RIGHT ANKLE
PT. HAS FOOT DISFIGUREMENT FROM CHRONIC COWBOY BOOT WEARING. DX:FOOT DISFIGUREMENT
PATIENT WAS ACCIDENTALLY KICKED IN RIBS PLAYING WITH FRIENDS WHOWORE COWBOY BOOTS. DX. RIGHT RIB CAGE STERNAL SOFT TISSUE.
Banana peels:
WALKING DOWN HANDICAP RAMP CARRYING BOXES AND STEPPED ON A BANANA PEELAND FELL STRAINING KNEE
32 YO FEMALE SLIPPED ON BANANA PEEL AND FELL TO FLOORKNEE STRAIN
PT SLIPPED ON BANANA PEEL AND FELL ON FLOOR IN STORE
I wanted to visually summarize the variation within sets of similar stories like these, and after tinkering a bit realized that this problem was very similar to a collaboration I was a part of a while ago that focused on visualizing variations across a set of lede sentences in newspaper articles. One of the goals there was to reveal authorial/media bias, which led us to stay close to the surface texts since phrase ordering and word choice are part of how bias is expressed. In the ER visit stories, though, the texts are written in medicalese and the event semantics matter more than surface syntax, so I think it would be fine to dramatically restructure the text if doing so reveals interesting higher-level patterns. It’s also possible that visualizing something like the temporal sequence of events and their consequences directly will wind up being a good idea here.
The story so far
After getting the dataset into shape I spent some time learning about minimal finite state acceptors, which I thought could be a mechanism for merging similar sentence fragments together. FSAs compactly represent a set of strings by reusing suffixes wherever possible:
Input:
Yuri accidentally went to the store
Ruby deliberately went to the store
Output:
Yuri accidentally ⤵
went to the store
Ruby deliberately ⤴
This post by Andrew Gallant has a great overview of FSA construction and usage. In the section on FSA construction Andrew visualizes the algorithm for constructing a minimum finite-state acceptor for a given set of strings. I implemented the algorithm described in the post, which comes from a paper called Incremental Construction of Minimal Acyclic Finite State Automata , and tried it out on some of the stories from the emergency room data.
My plan was to see whether FSAs could be used to capture the variation in a curated set of sentences based on a search term, such AVOCADO or BOOTS.
An issue that came up is that, since each node in an FSA represents a fixed set of strings, finite state automata will only compress strings if they share a suffix. For example, the following two sentences cannot be compressed using an FSA because they differ in their last word:
Yuri accidentally went to the bar
Ruby deliberately went to the store
One way around this is to focus the compression on a local neighborhood around the word of interest (eg. WENT above) and to build two automata: one for the prefix leading up to the word, and another for the reversed suffix of the word. The reversal of the suffix makes it so that the “end” of the FSA is closest to the word of interest, which often leads to a more compact automaton.
For example, here’s a pair of FSAs for BOOTS, visualizing local neighborhoods across 10 sentences: 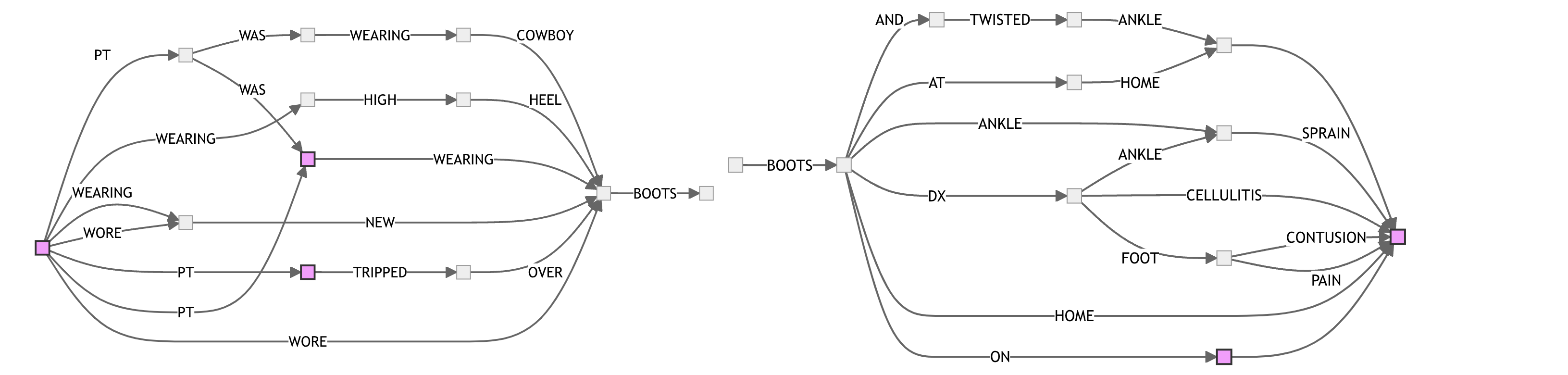
Here’s BOOTS with 20 sentences: 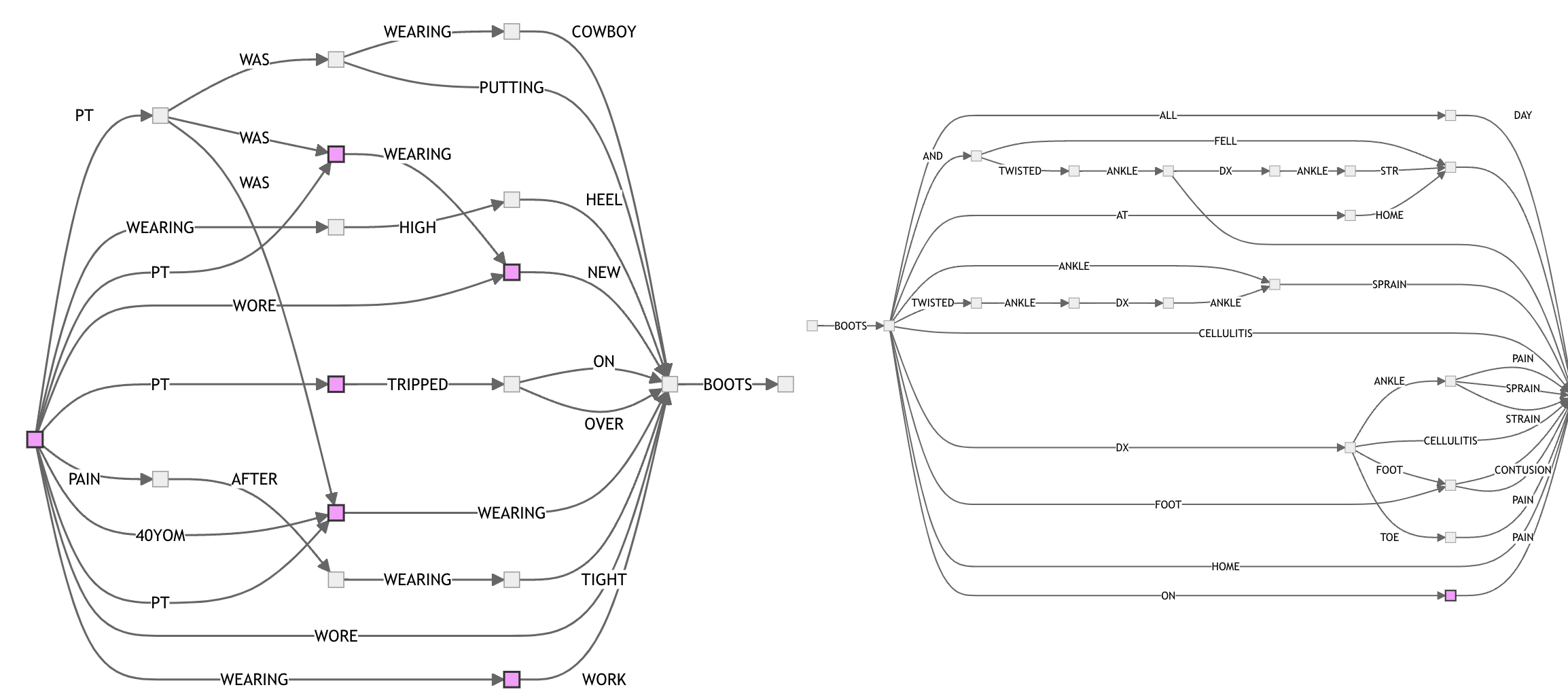
And here’s BICYCLE with 25 sentences: 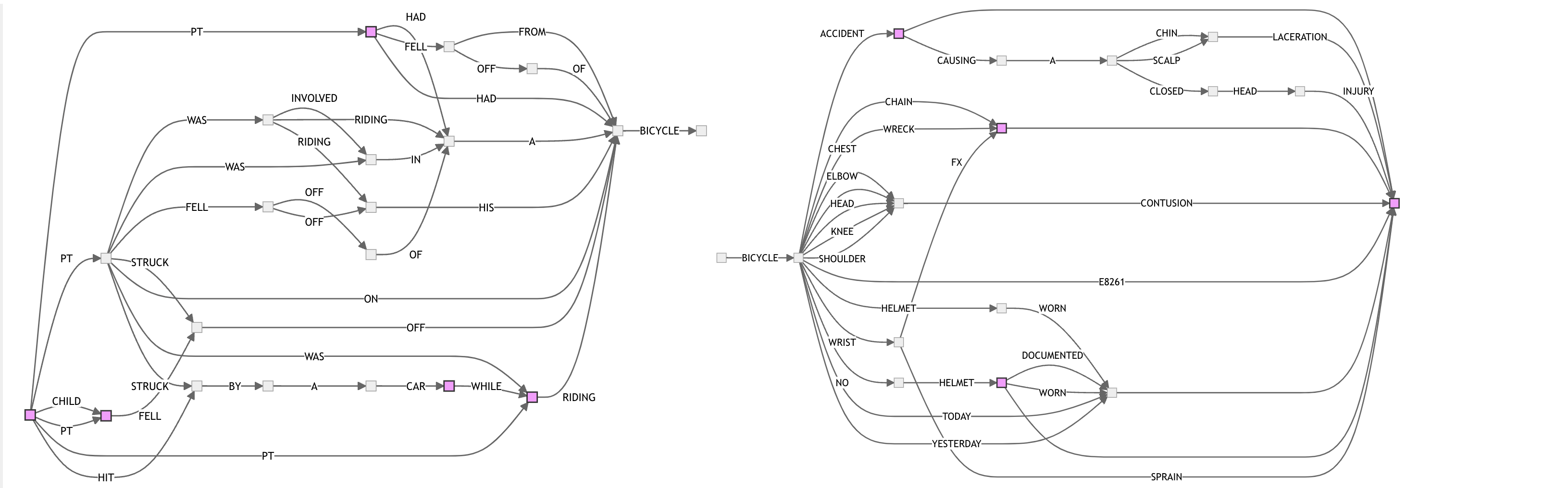
It feels like there’s a glimmer of promise here, but I need to do some more thinking about how to proceed.
One idea is to use LLMs to conform the sentences to a more standard structure, then build automata for each “semantic fragment” of the sentence, and visualize the result using something like a parallel coordinates plot with ordinal Y axes.
Another thing I want to try is to identify collocations (multi-word phrases like “christmas tree”) and use those as the elements over which the FSA is built, rather than always simple-mindedly splitting on word boundaries.
There’s also a lot of work to do on visual presentation. The current diagrams are just the raw output from Mermaid and are hard to read. Perhaps there’s a layout algorithm that is a better match for this family of graphs. My suspicion is that, in the end, the visualization should look significantly less graph-like, with the FSA graph serving as more of an inner structure to guide layout decisions. Related:
First there is old work by Book and Chandra, with the following abstract.
Summary. It is shown that for every finite-state automaton there exists an equivalent nondeterministic automaton with a planar state graph. However there exist finite-state automata with no equivalent deterministic automaton with a planar state graph.
I wonder if it would be reasonable to “planarize” nonplanar FSA graphs by duplicating nodes and edges. I’d like to make it easier to read these from left to right without so much eye movement, and being able to lay sentences out without intersection seems like it would help.
A few things this project reminds me of:
- The data is similar to that underlying some visualizations I worked on for large collections of distributed traces. For that effort we aggregated individual traces into a prefix tree, with edges representing service dependencies. (FSAs are compressed representations of prefix trees).
- One of the powerful ideas in that project was that we built service-centric views that merged together all of the prefix tree nodes for the target service in postprocessing, which is similar to what I did above in building the prefix trees for the prefix/suffix of a local window around the target word.
- Both forms of merging result in ambiguous graphs. I think this is fine so long as there is a way to disambiguate interactively – it could let us scale to much larger sentence sets.
- This post on dominator trees.
- The Gyllenhaal Experiment, which visualizes people’s attempts to spell a famous person’s name:
Creating a Visualization Library in Mathematica
Status: First draft; written in a hurry. Publishing since I want to get better at publishing incremental work and nobody reads these things anyways.
I recently came back to using Mathematica as my tool of choice for early-stage prototyping and data exploration. Unlike many other language ecosystems, Mathematica comes with a lot built in, including many data visualization functions. However, plots are scattered throughout the landscape without a high-level system unifying them: every new chart lives in its own world, and there’s nothing resembling The Grammar of Graphics unifying them.
So I decided to see how much work it would take to create a more uniform and flexible plotting system like Plot, my current tool of choice for browser-based visualizations, in Mathematica. It’s been a few days and I’ve made some progress and have the following picture to show for it:
Which was made by this code:
plot
The library works along very similar lines to Observable Plot, which is the existing library I’m most familiar with, and directly inspired this effort.
Technical notes
The following was written in something of a hurry, and I plan to refine it later.
The basic idea is that a plot is a collection of marks overlaid atop each other. (This plot has one mark, dot.)
A plot encodes meaning through visual channels, such as x or y or color. Each mark provides data to some number of channels. Based on this data, together with preferences provided by the user, the plot function comes up with an encoding for each channel that maps from the data domain to the visual domain (eg. taking a category label such as “a” and turning it into a color, or taking a numeric data value and turning it into a position along the x-axis.
The usability of the library depends strongly on the amount of deduction the library can make for you, and its ability to add explanatory marks to the plot, such as legends and axes, so that the resulting picture can be made sense of.
An interesting point that I had not sufficiently appreciated is the importance of representing scales in a way that allows you to make these explanatory marks. For example, the library needs to be able to tell when a log scale is used so that it can generate logarithmic axis ticks. Another example is that in Plot, the “shorthand” field specification syntax is what allows the library to know how to label your axes. A possibility in Mathematica is to use controlled evaluation for the same purpose.
This also raises some questions about evaluation order. I was hoping to use regular marks to build the axis legends, but had to figure out a solution to the time-ordering problem: Normal marks determine the set of inputs for each channel, from which scales for each channel are inferred, and ticks generated. But axis marks need to know the tick values. My current solution is to allow a mark to be a function which will be invoked with scale information. Any points plotted by such marks will not be used to determine the domain of the plot.
Another Plot design point that I hadn’t fully appreciated is that one reason it uses a z channel to allow eg. the line mark to make multiple lines is because sometimes one data column wants to be plotted as multiple curves, eg. with categorical time series, where you don’t want the user to need to reshape their data to calling your mark function.
My implementation so far is about 250 lines of code, and doesn’t yet include the ability to make bar charts, does not include faceting, or support for something like Plot’s z channel. I’m also not yet sure about the best way to support interactive selection, highlighting, and animated transitions. But you can use continuous, ordinal, and categorical encodings to plot text, dots, and lines, with scale and tick inference and a composable mark system.
We’ll see if my current design survives the addition of any of these new features. Part of the pleasure of using such a high-level programming language is that rewrites are cheap: when you know what you want to say, and if performance isn’t too much of a concern, you can express yourself very concisely.
References
Plot – My favorite plotting library, from the folks behind d3.
Wolfram Videos: ggplot: A Grammar of Graphics for the Wolfram Language – I came across this while writing this note. Haven’t watched it yet.
Appendix: Code
(* Names of all channels *)
= ;
(* Mapping from option names to channel names *)
= ;
(* Converts its argument to a list, if it isn't one already *)
:= If
(* "Broadcasts" scalar values in an association to lists, so the \
result is tabular in structure. *)
:=
AssociationThread
(* Normalization functions to rescale a domain to [0, 1] in the case \
of continuous and ordinal, or to [0, n] in the case of indexed *)
:= Rescale &
:=
AssociationThread
:=
indexed/Length - 1/
(* Map an association to another association: <| k->v |> -> <| \
k->f[k,v ]|> *)
(* This is a bit confusing, but have a look at its usage in mark \
render functions. *)
:=
AssociationMap
(* Applies the appropriate scale function to each option in assocs *)
:= kvMap
(* Returns a list of k->v where k is the channel name and v is a list \
of values *)
:=
mark // List // Prepend // KeyIntersection //
Values // Transpose // MapApply //
KeyDrop
(* Dot *)
:= Module
:= Association
Options[] = ;
(* Line *)
:= Module
:= Association
Options[] = ;
(* Text *)
:= Module
:= Association
Options[] = ;
(* Link *)
:= Module
Options[] = ;
:= Association
(* Axes are given as function marks, which accept the scales as an \
argument, and whose values do not inform the scale domains. *)
(* This solves the order-of-operations problem where the domain is \
inferred from marks, and wants to be "visualized" by axis marks. *)
(* We still need a way to signal to Plot to not add its own axes if \
the user provided some; maybe with some magic options. *)
:=
If &
:=
If &
(* Default color schemes *)
:=
Module
:=
Blend &
(* Scale inference fills in the subcomponents of a channel scale \
based on the channel, whether the values are numeric, and \
already-specified subcomponents. *)
(* Base case *)
:=
(* Default "out" for the radius channel *)
:=
(* Default domain for the "opacity" channel *)
inferScale :=
(* Default domain and normalization for channels with all numeric \
values *)
inferScale :=
(* Default domain and normalization for channels with nonnumeric \
values *)
inferScale :=
:=
(* Default continuous|ordinal color scheme *)
inferScale :=
(* Default indexed color scheme *)
inferScale :=
(* Default normalization is continuous *)
:=
(* Default out transform is Identity *)
inferScale :=
(* Tick inference figures out the ticks for a scale based on the \
properties of its subcomponents. *)
:= domain
:=
Range
:=
Range
(* Remove Null elements from a list, since it's a common mistake to \
call plot[mark1, mark2, ] with a trailing comma. *)
:= xs /. Null -> Sequence
(* The plot function accepts a list of marks, and returns a graphics \
object. *)
Options[] = ;
:= Module
= ExampleData;
= raw // Map;
plot
It depends what race you’re running
Imagine there are three teams of runners who are about to compete against each other in a team-vs-team race.
The first team has some very fast runners, but also some that are very slow. Despite the slowpokes, this team has highest average speed.
🯅 🯅 🯅 🯅 🯅 🯅 🯅
-----------------------------
Slow Fast
The second team is made up entirely of unremarkable runners, all of whom run at roughly the same middling pace.
🯅🯅🯅🯅🯅🯅🯅
-----------------------------
Slow Fast
The third team consists of runners who are far below average. But it has one incredible athlete – a world-class talent who’s easily the fastest runner on any of the teams.
🯅🯅🯅🯅🯅🯅 🯅
-----------------------------
Slow Fast
Which of these teams is most likely to win the race? Well, it depends entirely on what kind of race it is.
- It might be a relay race, in which the total time taken by a team is the sum of the times taken by the individual runners. In this scenario, the first team would be most likely to win since it has the highest average speed.
- Or maybe the race is one in which all of the runners start at the same time and teams are scored by how long it takes everyone on the team to finish the race. In this case, the time for a team depends exclusively on its slowest runner, which would give the second team the advantage since the other two teams both have slower runners.
- Or maybe teams are scored not by their slowest runner, but by their fastest. Then the third team would be the favorite since it has the fastest individual runner.
This analogy is an attempt to explain some simple but deep ideas in software performance that I came to relatively recently, despite writing software for more than a decade:
- It’s useful to think of the execution time of a program not as a number, but as a distribution.
- Which aspects of this distribution are worth optimizing depends not on the program, but on the context in which the program is invoked.
In the analogy, each team represents a computer program, and each runner represents a single execution of that program. The differences in the runner’s “run times” captures the idea of performance variation across multiple executions of the same program.
- The relay race is like a plain
forloop. Executions of the program occur serially, and the total time taken is the sum of the times of the individual executions. To win this race, it makes sense to optimize the mean execution time, which is just a scaled version of the sum. - The second race, in which all of the runners have to cross the finish line, is like invoking a program many times in parallel, then waiting for all of them to complete, as one might in a map-reduce computation. For example, imagine you want to search a partitioned dataset. Individual partitions can be searched in parallel, and then the results combined, with the total run time depending on the maximum time it takes to conduct an individual search (since you need to wait for the slowest search to finish before returning the combined results).
- The third race, in which the team with the fastest runner wins, is like issuing a bunch of parallel calls and but only waiting around for the first result. A practical example of this pattern is the idea of hedged requests where, simplifying somewhat, to improve the response times from a service you send it multiple identical requests and take the response that arrives first, ie. the one with the minimum run time.
References
Just as fault-tolerant computing aims to create a reliable whole out of less-reliable parts, large online services need to create a predictably responsive whole out of less-predictable parts; we refer to such systems as “latency tail-tolerant,” or simply “tail-tolerant.” Here, we outline some common causes for high-latency episodes in large online services and describe techniques that reduce their severity or mitigate their effect on whole-system performance.
Minimum Times Tend to Mislead When Benchmarking
In this short post, I want to make a simple argument against using the minimum time of a benchmark as a proxy for that benchmark’s performance.
Tail Latency Might Matter More Than You Think
I continue to believe that if you’re going to measure just one thing, make it the mean. However, you probably want to measure more than one thing.
This draft is based on ideas I learned about in discussions with Yao Yue, Dan Luu, and Rebecca Isaacs over the last few years, all of whom know way more about this stuff than I do and have written articles and papers that cover the same ground but in much more conceptual depth and technical detail.
Also, all this assumes that you care about winning the race in the first place.