January 2025

Enter the Wavelet Matrix

Imagine you have an array of integers and want to preprocess it so that you can answer quantile queries, such as computing the median or the 99th percentile, in constant time.

One possible solution is to sort the array and then answer the quantile queries by looking up the relevant entries in the array.

But what if, instead, I asked you to preprocess the array for range quantile queries, where rather than computing the quantile over the entire array, you want to compute quantiles for any sub-slice arr[i..j] in constant time?

Computing range quantiles involves combining information from both the original order and the sorted order, so sorting the entire sequence in advance no longer suffices. And the quickselect algorithm, which is often used for computing specific quantiles directly from an unsorted array, does not help us either, since rather than being constant-time its runtime depends on the length of the slice of the array.

Enter the wavelet matrix, a data structure that represents the process of sorting.

The wavelet matrix reorganizes the data in the array in a way that allows answering range quantile queries, and a lot more, in constant time:

You can access any element of the original sequence in its original order in constant time.
You can access any element of any slice of the array in sorted order in constant time.
You can count the number of times any element occurs in any slice of the array in constant time, which is known as a rank query.
You can count the number of times all elements occur in any slice of the array in constant time with respect to the length of the slice, with the runtime scaling with the number of unique elements that are counted.
You can find the location of any occurrence of any element of the array in close-to-constant time, which is known as a select query.
You can find all of the elements that occur more than X% of the time, in any slice of the array, in an amount of time that depends only on X and not the length of the slice. This is known as a k-majority query.

This all sounds very attractive, but there are some trade-offs.

The main downsides are that the data representation has some space overhead, on the order of 10-20% of the space required to store the bits of the integers themselves, and a high constant time factor due to the distributed nature of the data representation.

Internally, the wavelet matrix is composed of an array of bit vectors, each representing the bit planes of the original integers, which means that the bits of any specific element are scattered throughout memory and need to be reassembled as queries are executed, which hurts performance due to a lack of data locality and somewhat unpredictable access patterns, which can be somewhat alleviated by batching.

I’d like to explain more about the mechanics of how this thing works in the future, but for now there’s a great paper written by Gonzalo Navarro, one of the co-discoverers of the wavelet matrix, which serves as a great introduction of the basic idea along with a whirlwind of the literature around it. The article is called Wavelet Trees for All because the wavelet matrix is actually an optimized data representation for a conceptual tree structure called the wavelet tree. The word wavelet hints at the fact that the integers are decomposed into something like their frequency components, but no actual wavelets are used in the process of making a wavelet tree.

I’ll leave you with a picture I made a while back of an algorithm that constructs a wavelet tree through a series of incremental stable sorts.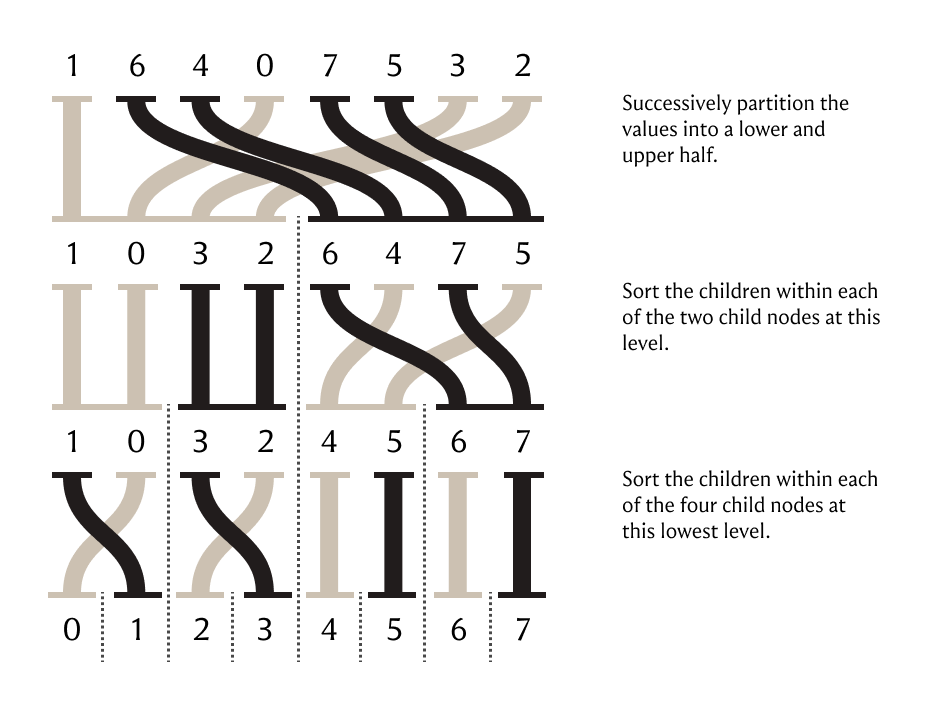

January 2025 Enter the Wavelet Matrix

Further reading

January 2025

Enter the Wavelet Matrix